Dr. Walsh received College of Science Faculty Scholar award for recognition of his exceptional contributions to his discipline and Oregon State University. This is a three-year titled endowed position. See more details at https://internal.science.oregonstate.edu/faculty-and-staff-awards/college-science-whiteley-faculty-scholar-teaching-excellence-award-and-osu
Category Archives: Teaching and Learning
Physics faculty honored at College Awards Ceremony
It was a banner day for Physics at the College of Science Awards Ceremony on Tuesday, February 22, 2022 (lots of twos, too).
Liz Gire won the Frederick H. Horne Award for Sustained Excellence in Teaching Science. A master innovator in teaching, Liz earns accolades for her skill in communicating difficult topics and her ability to pitch physics at the right level for her students. A student wrote, “Her level of dedication to the genuine support and inclusion of the students in her courses is something I’ve never seen in an educator before. She backs that up with her skill and experience in education and communication that makes difficult content still accessible and enjoyable to learn.” Read more at the College of Science Impact Magazine.
Matt Graham was presented with the Industry Partnership Award for his work on harnessing waste heat. Matt has worked with several companies over the past several years on projects that have led to Ph.D. theses for his students.
Davide Lazzati earned this year’s Milton Harris Award for his outstanding work in the field of high-energy astrophysics. His pioneering considerations of electromagnetic signatures of neutron star mergers hav produced some of the most detailed predictions of compact binary mergers, perhaps one of the most exciting topic in astrophysics in the past decade. Read more at Impact Magazine.
Heidi Schellman is this year’s Gilfillan Awardee. The F.A. Gilfillan Award for Distinguished Scholarship honors faculty members in the College of Science whose scholarship and scientific accomplishments have extended over a substantial period of time, especially faculty whose research careers have had a significant impact on his or her field. Heidi’s work in neutrino physics is just part of her work leading to 700 peer-reviewed publications and an h-index of 113. She has contributed to several well-known scientific collaborations and currently serves in a leadership position for the Deep Underground Neutrino Experiment (DUNE). Read more at Impact Magazine.
Changes to the Oregon State Physics graduate program
Oregon State’s Department of Physics recently underwent a major reform of their graduate program and requirements.
Introduction:
U.S. Physics Departments generally require that doctoral students complete core advanced courses in Quantum Mechanics, Electrodynamics, Classical Mechanics, and Statistical Mechanics, with additional electives depending on the field of study. Most Departments also require that all students demonstrate proficiency by passing written or oral examinations in the core topics. These examinations have different names (Preliminary, Qualifying or Comprehensive) but generally involve several multi-hour written tests. Students are normally given several chances to pass but if they fail to pass these examinations by the end of their second year, they are usually asked to leave the program.
At OSU, as at most Physics Departments, graduate students in their first 1-2 years are normally supported as graduate teaching assistants with significant teaching responsibilities while they are taking the required courses. As graduate and undergraduate courses start at the same time in the Fall, new graduate students typically find themselves teaching several undergraduate laboratory or recitation sections and taking three challenging courses, right after they arrive. The combination of a new environment, challenging courses, and teaching duties, all at once, can become overwhelming. Institutions can help with preparation, for example with pre-term orientation sessions, but the transition is still very difficult.
Oregon State physics recently did a major reassessment of the early requirements for our doctoral program which has led to three major changes.
First, entering graduate students are assessed individually by a group of faculty on arrival. The Core Graduate Advising Committee meets with all incoming students to assess their preparation for the Core graduate courses. Students who have missed a component (for example Statistical Mechanics) in their undergraduate preparation, or feel underprepared, are given the chance to take the appropriate undergraduate course in the first year, and then proceed to the advanced courses in the second year.
Second, the graduate teaching load in the first term has been reduced and the third core course for entering students is now replaced by a pedagogy course, taught by a faculty member with experienced graduate teaching assistants as mentors. This helps incoming graduate teaching assistants gain the skills they need very early in their graduate career.
Third, the written comprehensive examination has been replaced by a series of assessments over the first 2-3 years. These include the grades in the core courses and demonstration of written and oral communication skills. In particular, candidacy for the doctorate now requires a writing sample and a researched presentation on a general topic posed by the committee and communicated to the students several weeks before the exam.
These changes resulted from a multi-year process, initiated by both faculty and graduate students. Both groups realized that talented students were being lost due to overload in the first term or later, through failure to pass the written examination or, more often, out of worry that they would not pass after a failed attempt.
Inputs and proposed solutions:
Several years ago, a group of graduate students, led by students in the Physics Education Research group, researched and presented a paper on studies of known sources of bias in high stakes testing. In parallel, the faculty had long recognized that the skills needed to be a successful physicist were not solely correlated with an ability to take timed tests. Over the years, various reforms of the written examination had been tried, with little change in outcomes; talented students were still leaving the program. An elected graduate student representative committee was formed, with an elected (by the students) faculty liaison to provide input. A series of Town Halls led by the graduate representatives were held. At those Town Halls, students described their concerns about the program, in particular the sink or swim nature of the first term and the high stakes exams.
The faculty formed a committee of Associate Professors to recommend major changes to the doctoral program requirements. Their work was informed by Oregon State’s training in unbiased hiring practices and the modern methods they used in developing learning objectives and assessments for their courses. The committee spent most of a year formulating the learning objectives for a physics doctorate. 5 objectives were identified:
- Analyze Physical Systems Apply physical laws and principles to formulate and produce solutions to questions that arise from a broad range of physical phenomena; master quantitative techniques (exact techniques and various levels of approximation including order-of-magnitude estimates); and devise and adopt ways of making meaning of their results.
2. Learn Physics Expertly Learn and apply new concepts, methodologies, and techniques by identifying and engaging with various resources including, e.g., research literature and books, both individually and in collaboration with peers and other experts.
3. Create and Share Novel Physical Insight Design and conduct original research within a chosen specialty and disseminate the results through effective presentations in professional settings and in the scientific literature. Research expectations include: familiarity with primary literature, identification of central issues and knowledge gaps, ability to develop original questions, ability to identify and mitigate obstacles in research, ability to engage in productive discussions and work synergistically within a group or collaboration, and ability to write effective scientific publications that include citations and clear descriptions of methods and results.
4. Communicate with Learners Design and facilitate physics learning experiences at an appropriate level of sophistication for a broad range of audiences (e.g., colleagues, students, and the general public).
5. Do Physics Ethically and Inclusively Conduct themselves ethically and inclusively in all professional settings, in accordance with the American Physical Society code of ethics (https://www.aps.org/policy/statements/ethics.cfm), as well as proactively identify areas where ethical and/or discrimination issues may arise and articulate strategies for dealing with them.
Curricula and projects were then proposed to cover each of the objectives and new methods of assessing mastery were proposed. In particular, the committee proposed replacement of the written comprehensive examinations with grades in core courses and replacement of the general physics portion of the doctoral candidacy exam with a writing sample and a prepared pedagogical presentation on a set topic.
In addition, the first-year graduate curriculum and graduate teaching training were revamped to make the first year more inviting and flexible. The substantial faculty effort previously put into setting three written examinations per year was redirected into the expanded Core Graduate Advising committee to provide initial and continuing personal advising to beginning students.
Implementation:
A professional facilitator worked with the faculty committee to prepare for a retreat to discuss the new requirements. At the retreat, after considerable discussion, the new requirements were approved by consensus of the faculty. Graduate students were then given an opportunity to provide feedback on the proposed changes. Their comments were generally positive but led to several clarifications and improvements. The new system was voted upon in February 2020 and became the only policy for students arriving in the Fall of 2020. Most existing students who had not yet advanced to candidacy have also opted to follow the new program.
Preliminary Assessment:
It is early to do a full evaluation but preliminary feedback from 1st year students indicates that the flexible course scheduling and emphasis on training in the first term have had positive results. Core faculty were initially concerned that their new role as grading gatekeepers would work against their roles as champions for their students. However, the Core Advising Committee’s attention to student needs early in the program has led to increased student success in the core courses.
The doctoral qualifying process has become somewhat more complex with the addition of writing samples and set presentation topics requiring additional planning.
The new methods may lead to changes in admissions policy. Talented students with unusual backgrounds are likely to do better in the program, thanks to more intensive advising and flexibility early in the program. However, the absence of the required examinations may lead to greater attention to undergraduate grades as a predictor of ability in academic courses.
Summary:
Based on student input and faculty experience, Oregon State Physics has substantially modified the initial experience for incoming students and evaluation practices. Initial results are positive, with improved retention.
Astronomer in Residence Randall Milstein featured by Samaritan Hospital
OSU Astronomer in Residence, Senior Physics Instructor and man-about-Corvallis Randall Milstein has been featured by Samaritan Hospital in an article and a huge billboard on OR34. See https://www.samhealth.org/randallm for the full article. You can meet Randy in person in Physics 104 (Descriptive Astronomy), the class he teaches to hundreds of students every term at Oregon State.
David Roundy’s PH366 Computational Physics Lab models epidemic like COVID-19
When the novel coronavirus pandemic hit, the Physics Department, like the rest of Oregon State University, scrambled to get its course offerings ready for remote learning in a few days. Professor David Roundy and his teaching team scrambled as hard as anyone – and incorporated some beginning epidemic modeling into the computational physics class so that the students would begin to acquire the skills that will serve them well as members of the technological community of which they are now junior members.
About the class:
PH366 – Computational Physics – is a course in which students learn how to solve mathematical equations in real-world, complex situations where analytical, “pencil-and-paper” solutions are far too difficult. For example, it’s easy for a student in Introductory Physics to solve a simple differential equation to find a solution in the form of an equation that describes how a ball falls towards the earth under the influence of gravity, a constant force near the earth’s surface. But add extra forces that describe real conditions like air resistance, wind and the earth’s rotation, and a simple equation to describe position as a function of time is impossible. The computer solves the problem numerically, chopping it up into very small time slices and finding a position and velocity for each of the times based on what is was at the previous time. In the PH36x Computational Physics series, students learn techniques to find numerical solutions to many differential equations and they can explore very complex, real-world situations. Roundy has chosen the Python programming language for this class, but the lessons are applicable to any language. In real physics research, few problems are already worked out in a textbook and numerical methods to solve them improve all the time, so the best information is often distributed all over the internet. Physics students must learn to navigate the body of existing literature and identify what information they need to solve a problem.
Another view of the solution shows the difference between displaying results on a linear plot and a logarithmic plot. The logarithmic plot (below) highlights the infection and recovery numbers, which are a small fraction of the overall population and we’d be tempted to ignore the fact that there are hundreds of thousands of sick people if we saw only the linear plot (above).
An example that David Roundy chose for the Spring 2020 Computational Physics course was about the spread of an epidemic, like covid-19. It was all everyone was talking about, and he wanted the students to learn how their new computational skills are at the heart of epidemiological modeling that gives us the information to understand and mitigate the spread of the coronavirus. This isn’t an accurate model, Roundy stresses, but it has valuable elements – start with a simple model, probably unrealistic, test it, make sure it works as expected. Add some complexity, test that, and then proceed. In his easy-to-read description at the PH366 course website, Roundy shows students how to model exponential growth – the increase in number of covid-19 cases is proportional to the number of cases: dI/dt = RI. Then you have to add in the real-world fact that the population is finite (with a doubling time of 1 day, the world human population would be infected in a little over a month). Some people recover and have immunity (we hope), so that must be factored into a more realistic model. More complexity comes in when you consider how long infected people are contagious, and whether there is a period of immunity following recovery.
Actually, the problem is not too hard to set up – it’s the solution that becomes tedious. That’s the beauty of computers is that they don’t care about tedium. They swiftly toil through tedious calculations without becoming bored or tired and their error rate is effectively zero! The humans have to set up the problem correctly, though, otherwise the results are meaningless. And this is the skill that Roundy teaches his students. The screenshots below show an example of the students’ work in PH366, with the by-now-familiar plot of an exponential rise in infections at the start, with a peak and fall. We see the basic recovery and death trends, too.
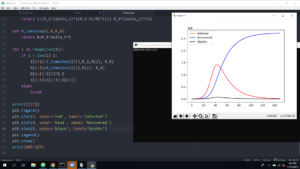
Another view of the solution shows the difference between displaying results on a linear plot and a logarithmic plot. The logarithmic plot (below) highlights the infection and recovery numbers, which are a small fraction of the overall population and we’d be tempted to ignore the fact that there are hundreds of thousands of sick people if we saw only the linear plot (above).
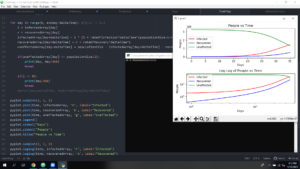
Julian Wulf, one of the Physics majors currently in PH 366 commented, “My favorite part of the class is how it allowed me to model physical situations that were too complex to picture, or model by hand. I have found it quite rewarding to finish coding something and have it modeled in front of me, a model that is often easy to adjust to new circumstances.” It’s easy to see how Julian would relish the challenge of modeling a much more complicated solution that factored in even more complexity such as social contact and real transmission rates.
Teaching in the age of coronavirus:
To deliver PH366, David Roundy goes into Weniger Hall by himself every Tuesday and Thursday and turns on some 20 computers with separate Zoom sessions running (see the panorama view below). The 40 students and the 4 TAs (teaching assistants) log in from their remote locations. The students implement Roundy’s “pair programming” strategy where they decide how to solve the problem and code in pairs, each providing the crucial check on the other to ensure that the steps make sense. They constantly question their results, and look up techniques to improve their code and to interpret the results. It’s a real-world programmer situation! Roundy and the teaching assistants hop between the Zoom breakout rooms to discuss with each pair of students how to troubleshoot and debug their code. It wasn’t easy for the instructors to change their mode of operation from in-person to remote learning. TA Elena Wennstrom comments, “At the beginning, our TA meetings were devoted to brainstorming possible class formats, testing the limits of our Zoom powers, and discussing issues and possible improvements to the class we had the day before. Now we are more able to focus on the content, and trying out the assignments ourselves (like usual). I’m really proud of the system we’ve developed. Classes go surprisingly smoothly, and the time flies.” Wennstrom adds that she gets more and better questions from the students in the remote mode. Roundy remarks that he will offer this new mode of teaching to students with seasonal influenza in “normal” times to help curb the spread of that particular virus.
The students’ response:
The students agree. Julian Wulf says, “I think the transition to remote learning has mostly gone smoothly. There has been a rapid increase in how well things are being communicated remotely, as well as an increasing ability of the teaching assistants and professor to respond to difficulties we encounter while programming. I find myself looking forward to the continued improvement as each class has run more smoothly than the last, with the teaching assistants and Professor Roundy being increasingly able to react to difficulties people encounter by jumping in and out of Zoom breakout rooms to help.”
As “newbie programmer”, Wulf feels that the pair programming method helped him get over an initial fear of programming, and that he has learned to appreciate how quickly he learns to solve new problems. He found the disease and epidemic modeling project interesting, intellectually stimulating and fun.
Wulf says that the coding skills he is developing will be useful in the future, and that they have already entirely changed his perspective. He now routinely plots equations in Mathematica to visualize a physical situation, and his new skills make the task “pain-free” and fun rather than being as a dreaded chore.
Former Physics major John Waczak, now a graduate student in Physics at the University of Texas at Dallas, offers similar observations about the Computational Physics series. He says that Computational Physics is an incredibly powerful tool for building physics understanding and to tackle problems that are otherwise unsolvable. It also enables him to create detailed visualizations of just about anything, and those visualizations don’t have to be static! Computers makes it possible to manipulate 2-, 3-, and even 4-dimensional data and create animations. “I have been using this skill a lot lately to visualize results in my [graduate] classes,” he says. Waczak further appreciates that PH36x made him an autodidact. “Dr. Roundy encouraged us to become familiar with the documentation and common programming forums like Stack Exchange. Instead of giving us working code to start with, we had to learn how to diagnose bugs and navigate the wide variety of (often incorrect) answers that exist online.” This meant that he became better programmer (and physicist). “I certainly do not know all of the tools and features that exist in the python programming language. What I do understand is how to evaluate the credibility of a resource and how to extract what’s important from the large body of existing information.”
Prof. Roundy’s PH366 covid-19 assignment is available at http://sites.science.oregonstate.edu/~roundyd/COURSES/ph366/epidemic.html
The TAs for the class are Elena Wennstron, Kira McCoy, Alex Kuepper and Steven Neiman.
David Roundy is an Associate Professor of Physics at Oregon State University, and has been teaching and researching at OSU since 2006. His work in computational physics spans exotic superconductors, metal-organic frameworks, classical and quantum density functional theory, biological motor proteins and many other topics. He invented the Darcs version control software. He is a member of the Paradigms in Physics team with significant funding from the National Science Foundation for education-related research focusing on thermal physics and computational physics.
Coronavirus update from the Department Head
Dear Physics community,
Oregon State Physics is still operating, although our labs are in standby mode and our teaching is now all remote. We’re using online channels like Zoom and Slack to maintain our tradition of student interaction in courses. Students are still working together on problems and the Society of Physics Students is launching an online game night. We could not have done this without herculean efforts by faculty and students to create online labs, videos, and sophisticated live classes in 3 weeks. Grad students are writing new labs and undergraduates are serving as learning assistants in the Virtual Wormhole. See this video on vectors produced in our Lightboard studio to see what our students see.
On campus, research is on standby. Biophysicists Weihong Qiu and Bo Sun led the Physics effort to collect personal protective equipment (PPE) that Oregon State then donated to Oregon Emergency Management agencies. https://today.oregonstate.edu/news/oregon-state-collects-nearly-200000-pairs-gloves-other-medical-supplies-covid-19-crisis But, you can’t grow carbon nanotubes or cancer cell lines at home so on-campus research is now on hold. In the short run, we can work on writing things up, doing the literature searches we never have time for and analyzing data, but we’re eager to get back to our labs.
If you are interested in helping students financially in the short term, Oregon State has set up an emergency fund for students in need. Many students (or their parents) have lost their jobs and are struggling with basics like books, rent, food and the now vital internet connection. Please consider donating to the Beavers Care fund which is providing emergency funding to OSU students https://app.fundmetric.com/qvRUQF9u4 (You can designate the College of Science) or to the Human Services Resource Center (HSRC) https://studentlife.oregonstate.edu/hsrc which provides food boxes, loaner computers and other emergency supplies for students.
We’ll be providing updates as things progress.
Heidi Schellman
Physics is working remotely
As part of Oregon State University’s COVID-19 mitigation plans, most Physics activities are moving to remote access.
Courses will be taught via remotely starting March 30: https://learn.oregonstate.edu/keep-learning
Colloquia and Seminars will also use video connections
We’ll keep you updated as we know more.
BioHealth major Haelyn Epp and Qiu Lab featured in Impact
Physics research isn’t just for Physics majors. Biophysicist Weihong Qiu hosts students from BioHealth Sciences and Biochemistry in his lab as well.
BioHealth student Haelyn Epp used her #SUREScience scholarship to work in a biophysics lab on motor proteins. “My scholarship replaced one of my jobs, [and] allowed me to focus on research in a way I had not been able to,” says Haelyn. Read the full article at:
Graduate Student Robert “Jake” Jacobs wins a NASA FINESST Award
Robert “Jake” Jacobs has been awarded a NASA Future Investigators in NASA Earth and Space Science and Technology (FINESST) award for 2019 in the competitive Earth Science Division. With this award, he is developing a method to analyze latitudinal circulation utilizing satellite measurements of ocean surface vector winds measured by the QuickSCAT and ASCAT scatterometers. Our objectives are to improve understanding of climatological atmospheric circulation patterns and how surface winds in the tropical Pacific influence El Niño-Southern Oscillation (ENSO) events. Latitudinal circulation plays an important role in weather and climate variability as it shapes where precipitation falls and how heat moves from the equator to polar regions. Improved accuracy of the boundaries between large-scale atmospheric cells can advance our understanding of climate and weather models.
Robert “Jake” Jacobs has been awarded a NASA Future Investigators in NASA Earth and Space Science and Technology (FINESST) award for 2019 in the competitive Earth Science Division. With this award, he is developing a method to analyze latitudinal circulation utilizing satellite measurements of ocean surface vector winds measured by the QuickSCAT and ASCAT scatterometers. Our objectives are to improve understanding of climatological atmospheric circulation patterns and how surface winds in the tropical Pacific influence El Niño-Southern Oscillation (ENSO) events. Latitudinal circulation plays an important role in weather and climate variability as it shapes where precipitation falls and how heat moves from the equator to polar regions. Improved accuracy of the boundaries between large-scale atmospheric cells can advance our understanding of climate and weather models.
This type of work while exciting is not new, as astronautical projects have been a driving force in Jake’s life. His passion for space has taken him from an undergraduate degree in Aerospace Engineering, from Purdue University, to satellite remote sensing at Oregon State University (OSU) where he is completing a PhD in Physics. Before arriving at OSU, Jake obtained a master’s degree in physics from Eastern Michigan University (EMU). While there, he worked with funds from the NASA Space Grant to develop an ion source that would be used in sputtering experiments to model the solar wind.
Connecting with his advisor, Dr. Larry O’Neill at OSU, has created an excellent partnership, as they bring different strengths to the table. Dr. O’Neill’s wealth of experience has helped Jake to greatly advance his knowledge of atmospheric and oceanic sciences. While Jake’s physics and math background have assisted with advancing spatial derivative analysis techniques. This newest project has combined Jake’s passion for physics and math with a novel astronautical venture. He greatly looks forward to continuing this project with the support of the FINESST Fellowship.
In his limited free time, Jake enjoys reading, hiking, swimming and playing disc golf with his two small children, wife and two dogs. An extra joy in his life is watching his children grow to love the universe and all its boundless opportunities. The family also enjoys star gazing, which can be difficult in Oregon, so they use a home star theater system to learn about space, stars and the world above.
Student Profile: A senior’s gut decision in high school to major in physics holds steady four years later
Reposted from impact.science.oregonstate.edu
A senior’s gut decision in high school to major in physics holds steady four years later
Looking back on his gut decision in high school to major in physics after taking a class in it, graduating senior Abe Teklu remains somewhat mystified. “I guess I was just really confident,” he laughs.
Abe grew up around numbers and changing locations, moving from Ethiopia to Arizona at age six when his father got an engineering job at Intel, and then moving to Colorado before his family settled outside of Portland when he was 12.
His family is mathematically inclined. His mom is an accountant and his dad, who not so secretly yearned to be a mathematician, is an engineer who reads calculus books and earned a master’s degree in fluid dynamics. This home field advantage explains some of Abe’s youthful confidence (he “loved math” even as a child) but since then Abe has carried the ball all on his own.
At Oregon State as an Honors physics student, Abe has remained confident – at least most of the time – as well as comfortable with numbers and shifting contexts. He has had three research internships. The first was the summer after his sophomore year when he had a paid internship at Northwestern University’s Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA) in Evanston, Illinois, in a rather niche but fascinating area of speculative research called astrobiology. There Abe analyzed mathematical models of theoretical predator-prey systems not limited to planet Earth.
The summer before his junior year, Abe headed down to San Diego for another paid internship, this time at the U.S. Department of Energy’s DIII-D National Fusion Facility. The facilty consists of a tokamak, a magnetic fusion device which Abe describes as “a big metal donut spinning plasma to get fusion energy.” Abe used magnetohydrodynamics (MHD) theory to model plasma confinement, with the goal of understanding which conditions better spread heat flux in the divertor region.
In his third research experience, Abe spent more than two years working in physics department head Heidi Schellman’s Particle Physics Research Group, analyzing neutrino-antineutrino data as part of the MINERvA, a major international research effort exploring matter-antimatter differences in neutrino physics. This involved aiming a beam of neutrinos from Illinois to South Dakota. Specifically, Abe worked on the recoil energies recorded when the rare neutrino-antineutrino reactions hit parallel strips of the scintillator, each of which is connected to a photomultiplier tube that determines how much energy is deposited in a strip.
Abe’s research experiences beyond the classroom gave him many advantages. For one, the DIII-D fusion internship formed the basis for his senior thesis. He also learned valuable lessons about the nature of scientific work.
“Unlike class, where there is always an answer, research is open-ended. It was difficult for me at first, but I came to appreciate that even if you don’t solve a problem, you are contributing to a much larger research effort with scientists around the world that will one day lead to a solution.”
Throughout his four years at OSU, community and relationships were key to Abe’s success, a sentiment reflected in his two top pieces of advice for new students.
“Have as much fun as you can freshman year. Talk toeveryone. You will have the most free time this year and so it’s a great time to meet new people and make friends. It gets harder after that.”
As an Honors College freshman, Abe enjoyed meeting friends in his dorm, Cauthorne, and also hung out in West so often that he was mistaken as a resident. He was and is “surprised by the amount of really smart people here. So many amazing people – and it’s so cool now to see all of my friends going off to exciting new destinations next year, from MIT to Brown to AI research!”
His second piece of advice?
“Talk to professors. Go to office hours. Not just to talk about academics, but just to talk about life. It’s helped me out a lot.”
Some of his favorite professors to hang out with are physicists Corinne Monogue, who he calls a “great teacher and person to talk to about anything at all” and Heidi Schellman. Abe suggests another good reason to talk with professors: It’s a “great way to start research sooner.”
To wit, when Abe visited to Schellman during her office hours, she began describing her research and Abe just jumped in and asked if he could help.
“That day she gave me a key to her lab and I started doing research!” Two years later, Abe still has a coveted seat in Schellman’s Lab and is currently mentoring a new student to take his place after graduation.
Despite his success at OSU, Abe has faced his share of rejection and challenging times. Before joining the Schellman Lab, he was turned down as a freshman for research positions. The fall of his senior year was a really difficult time. After an intense summer working at the fusion facility DIII-D in San Diego, he returned to campus for a nonstop term which on top of his usual demanding coursework included studying for the Physics GRE, applying to graduate schools, writing his senior thesis and dealing with the inevitable “personal stuff.”
“I was overwhelmed and my confidence was shaken. Was I good enough? I had imposter syndrome. The only thing that got me out of it,” Abe reflects, “was just to endure. I just kept going step by step, every single day. I had to keep going and I did and it finally got better.”
It certainly did. Abe was accepted into the physics Ph.D. program at Stonybrook University in Long Island, New York, remarking with great enthusiasm upon the fact that there are no less than “60-70 physics researchers there!” Not wasting any time, he will jumpstart his graduate research this summer at CERN in Geneva, Switzerland, working on a yet-to-be-defined research project with his graduate advisor.
Abe is grateful for the science education he has received at Oregon State and was not surprised when he heard that the Department of Physics recently received a national award for improving undergraduate physics education.
“All of my professors were great,” he said. The junior-year Paradigms in Physics series in particular, which was redesigned to include interactive pedagogies and real-world applications to better reflect how professional physicists think, was a real game-changer for Abe.
“[The junior-year Paradigms in Physics] was hard, but it was great and everyone in the class bonded together. We came out feeling that we could do anything!”
Abe’s gratitude extends to the many scholarships he received that helped cement his choice to go to Oregon State. He received the university’s four-year Academic Achievement award as well as a freshman year Honors College scholarship, a Kenneth S. Krane Scholarship in Physics and a David B. Nicodemus Scholarship in Physics.