First post on this blog! Let’s make it a good one 🙂
One personal project of mine is a multiplayer game web app. To play with friends, users enter a room code, which is a four digit sequence of capital letters, i.e. “XFGP”. Currently, all game data is stored in memory on the server, which functions adequately for my purposes, but in the interest of growing as a developer I have been working on moving storage of room and game state to a database. In the process of planning this change, I discovered a moderately clever way to handle room codes, and this post will chronicle the process of exploration and iteration.
What I Started With
My initial method was, like so many initial solutions when programming, a solution that works well enough for my purposes but was not the most elegant or efficient. As the code snippets below illustrate, my initial method does the following:
- Generate a random 4-letter code
- Check whether the code is already in use.
- If the code is already in use, start over.
- If the code is not already in use, we have found our new room code.


This method works, but it also has some flaws. Most apparent is the use of a while(1) loop that is not guaranteed to ever exit. Of course, to be trapped in this while loop forever, I would need 26 ** 4, or 456976 active rooms, which is a fairly large number.
A far more a pressing issue is that as the number of rooms increases, the expected number of tries it takes to generate a code not already in use also increases. This quality should be avoided when possible–the more rooms that exist, the heavier the load on the server will be simply due to player activity. I do not want to exacerbate the strain by having the complexity of generating a new room scale with the number of existing rooms, and by extension be directly correlated with existing load on the server. A search for an O(1) solution is in order!
A First Iteration
SQL databases are great at ensuring rows get unique integer identifiers by using attributes such as AUTO_INCREMENT (MySQL) or SERIAL (PostgreSQL). Perhaps we can let the database handle the creation of a unique value and translate these values into room codes? We can, and I played around in Python to generate a proof of concept.
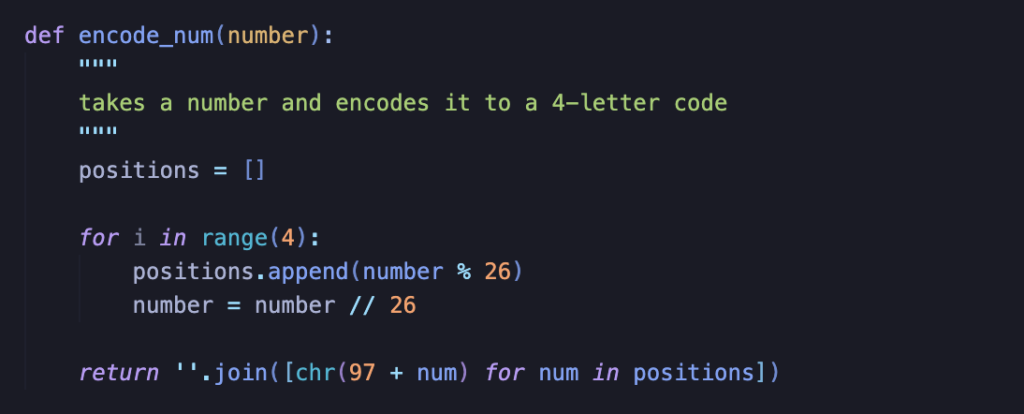
This method fundamentally relies on integer base conversion. You may recognize the process from times you have converted to or from hexadecimal. The basic idea here is the same, but we are instead converting a decimal (base 10) integer to base 26, and each resulting numerical value is represented by a letter. A = 0, B = 1, and so on, all the way up to Z = 25. And because the integers we are starting with are unique thanks to our database, the codes we come up with are unique as well until we reach 26 ** 4 codes generated! We can even verify that this method works by generating the entire set of codes in order and checking for duplicates, as I did in the program below:
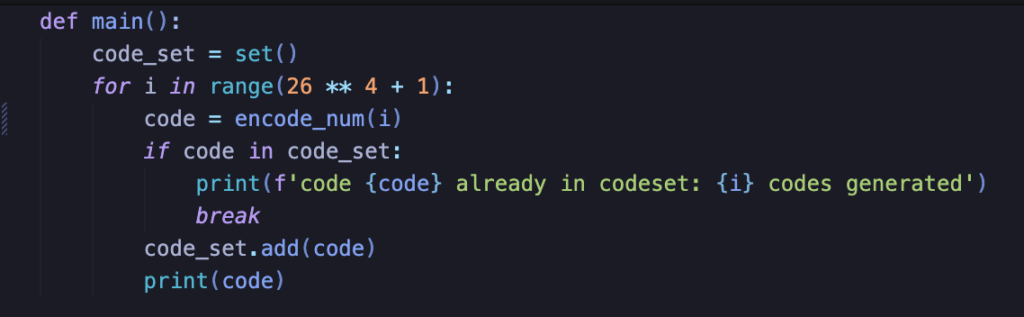
If a duplicate code shows up before we have generated 26** 4 = 456976 unique codes, the loop will break and we will be notified. Let’s run it and see what happens:
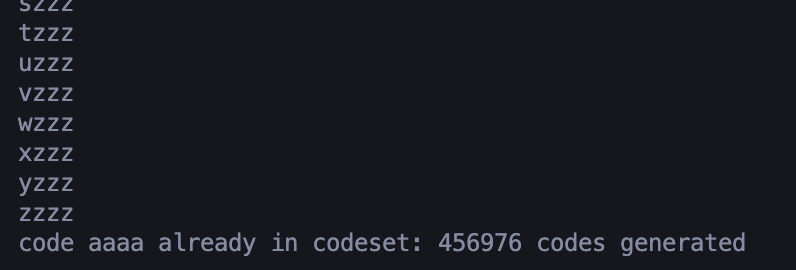
Success! The loop only breaks once 456976 codes have been generated! We can allow our database to handle generating unique room identifiers without the need for random guesses and then simply translate these unique identifiers into 4-letter codes! However, there is a drawback to this method. Observe that all codes generated within a sequence are incredibly similar:
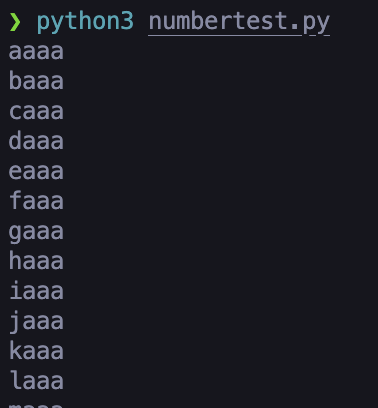
It stands to reason that codes based on sequential numbers will be similar. The numbers 456, 457, 458, etc. share similar numerals–of course a mere change of base will preserve similarity! This presents a minor problem. I plan to automatically delete rooms around 30 minutes after users last interact with them. As a result, with my initial random generation scheme, a user who mishears the code “BJKY” as “BJKI” will likely receive a message that the room they have attempted to join does not exist because the room codes should theoretically be evenly distributed. In contrast, with the integer base conversion scheme, a user who inputs “BJKI” instead of “BJKY” will likely unintentionally enter an existing room due to the closeness of sequentially-generated codes. Entering a valid but incorrect code and entering the wrong room rather than being informed that no such room exists is a more inconvenient experience for everyone involved.
A Better Solution (or, Finally! Prime Numbers!)
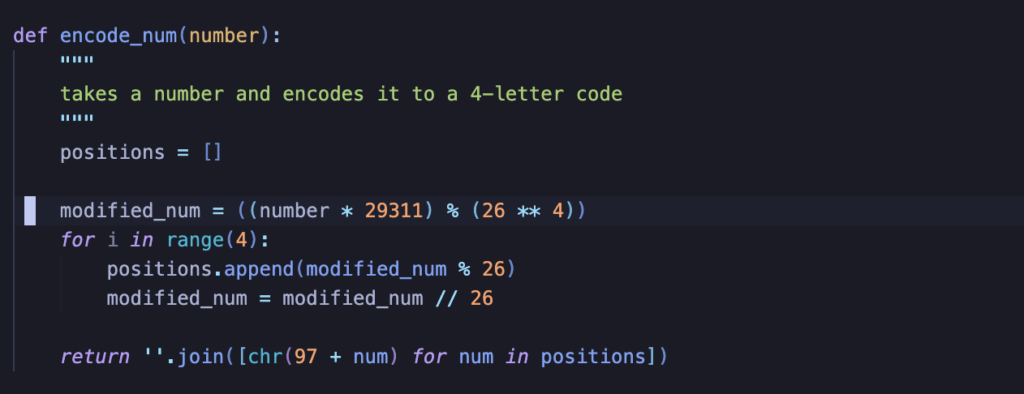
Using intuitions about prime numbers, I came up with a solution that preserves the constant-time advantage of the sequential solution and removes the drawback of sequentially-generated codes being too similar. It involved a minor change to the encode_num function that resulted in a large difference–the magic happens on the line with the cursor on it:
I’ll show the results of running the proof-of-concept program and then explain what is going on:
26 ** 4 = 456976 unique codes generated? ✅
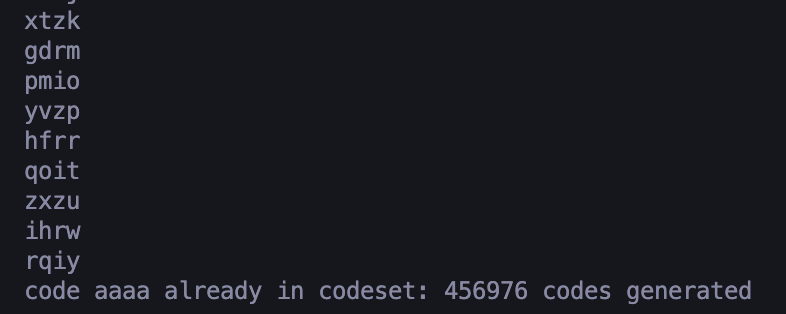
Sequentially-generated codes sufficiently dissimilar? ✅
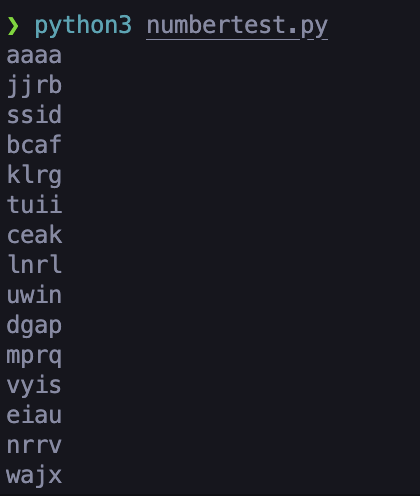
So what is going on? In the simplest terms, we are essentially no longer incrementing by 1–we are incrementing by 29311. Or rather, the database will still increment by 1, but the process of generating a room code from the number provided by the database will multiply that number by 29311 and perform modular division over 26 ** 4.
What’s so special about the number 29311? Two main things.
First, it’s a large enough number that incrementing by it changes all of the “digits” of the room code–recall that a 4-letter room code is essentially a base-26 number. When we were just adding 1, we were only changing the ones place on that base-26 number, but with 29311 we are changing all places.
Second, and requiring more explanation, it’s a prime number and therefore relatively prime to 26 ** 4. In other words, it shares no common factors with 26 ** 4. This property is what ensures the uniqueness of generated codes. For the sake of illustration, let’s look at the output of the proof-of-concept function when we change 29311 to 26000, which shares many factors with 26 ** 4:
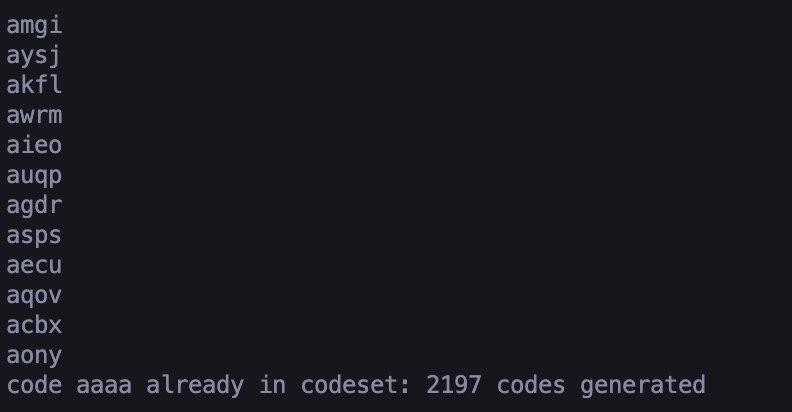
Because 26000 is not relatively prime to 26 ** 4, we don’t make it too far until we repeat a code–only 2197 codes were generated before a repeat!
Proof Time!
With examples out of the way, now it is time for a proof. When I implemented the solution, I was mainly working off of intuition, and I only later came up with the proof that provides some explanatory power for how my solution works. Hopefully this helps illustrate why the codes we generate are guaranteed to be unique until the entire set of possible codes has been generated. The following proof should be accessible with some knowledge of modular arithmetic and the properties of prime numbers:
Assume two positive integers, a and b, are distinct. Assume WLOG that a – b is positive. Now assume there are relatively prime integers p and q such that
ap mod q = bp mod q.
By the properties of modular arithmetic, this implies that there exists some integers j and k such that
ap + kq = bp + jq
and therefore
ap – bp = jq – kq
and
p(a – b) = q(j – k)
Now we get to use a pretty powerful theorem: the Fundamental Theorem of Arithmetic, which states that every integer has a unique representation as the product of primes.
Because p and q are relatively prime, we know that each and every prime factor of q is not in p. However, because
p(a – b) = q(j – k)
each side of the equivalence must share the same prime factors. Therefore, each prime factor of q must be a prime factor of (a – b), meaning a – b can be represented as cq for some integer c.
Because we assumed a and b are distinct, a – b is not 0 and therefore cq and c are not zero, meaning a – b is a non-zero multiple of q.
In other words, there exists some non-zero positive integer d such that
a – b = dq
so it can be concluded that a and b are at least q integers apart!
This explains why we can be assured that integers in the range [0, 456975] will generate unique room codes. In this scenario, a and b are the unique integers we receive from the database using AUTO_INCREMENT or SERIAL, q is 26 ** 4 (= 456976), and p is our arbitrarily-chosen relatively-prime-to-q 29311. Not only does the solution work, but we can see why it works!
Conclusion
Hopefully I have told a compelling story about iteration, improvement, and problem solving. It is rewarding to be able to utilize mathematics to come up with a solution to a problem.

Leave a Reply