FFT and IFFT Implementation
This week I was able to implement FFT, and IFFT functions into my program. I proved to myself that it was working by printing out the original time-based real data, followed by FFT transform of that data, followed by IFFT transform of the frequency data. I was excited to verify that the original time-based signal was reproduced as shown in the pic below. I verified the results printing portions of the time sequence at the beginning, middle, and end of it.

Pitch Shifting, and Time Stretching
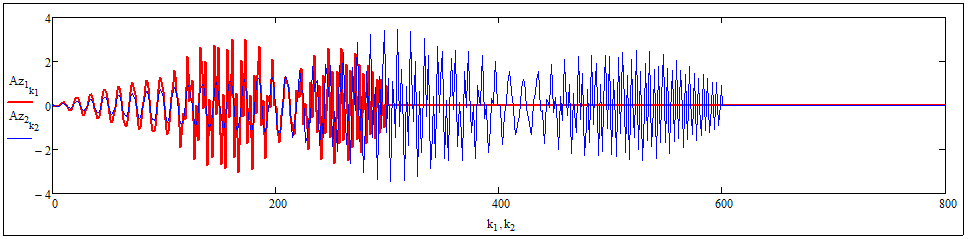
It occurs to me that pitch shifting (while keeping time), and time stretching without changing frequency may not be as easy as I thought. I will have to return to MathCad and study that concept some more. One problem I have is that when using FFT, a number of points that is a power of 2 is used. That means, I will have to zero-pad a time-signal at the end with a zero signal prior to entering into an FFT routine. How does that zero-padding with FFT compare to just FT without zero-padding. I must study this and understand it.
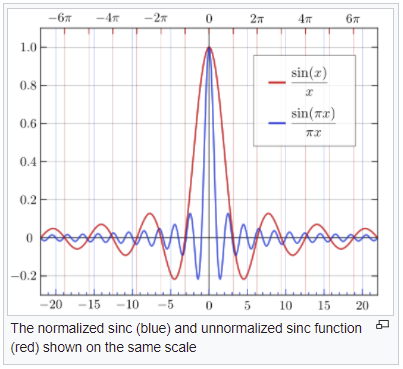
I may encounter sinc function considerations as I do this, as the above functions can be thought of an arbitrary time signal multiplied by a time-shifted step function that is initially 1, and then 0 after the signal is played. This would be equivalent to zero-padding.
O(N-N) or O(N-log(N))
Will pitch shifting while maintaining time, and time-stretching while maintaining involve convolution? If so, the run times will tend to N-squared. If not then then run times can remain as N-log(N). If convolution is unavoidable, then I may be better off not using Fast Fourier Transforms that would need 0-padding. I should just use Fourier Transforms since N-squared run-times become unavoidable.
It’s time to do some simulations. This time I will use a single frequency sine wave run over part of a time interval, after which it is turned off to simulate 0-padding. I must then determine what happens in frequency space during pitch shifting, and time-stretching.
